Come lo studio di un fiocco di neve a Capodanno può migliorare la trasmissione dati

Da una strenna giocosa di Capodanno viene fuori una congettura che tiene sulla corda i matematici per quattro secoli; ma come sottoprodotto di questi studi si ottiene un fantastico metodo per la trasmissione di dati con correzione automatica di errori. All’origine di tutto c’è Johannes Kepler, quello delle leggi del moto dei pianeti.

Keplero vuol fare un omaggio, per il Capodanno 1611, al suo benefattore Johann Matthäus Wacker von Wackenfels. Non si sa perché costui passi per un amante del Nulla (“Cum non sim nescius, quam tu ames Nihil”), ma Keplero introduce il trattatello De nive sexangula proprio come se fosse il frutto di una sua ricerca di qualcosa che sia il più possibile vicino al Nulla. Mentre attraversa il Ponte Carlo a Praga gli si posa sulla manica un fiocco di neve. Ecco un buon tema da offrire a un devoto del Nulla!

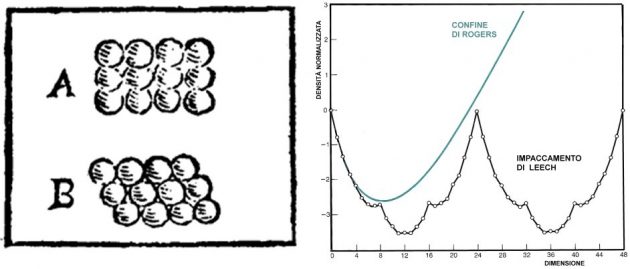
Keplero si lancia in diverse idee su come si produca la simmetria esagonale dei cristalli di neve. Principalmente ritiene che la causa possa risiedere nel modo in cui le particelle di aria satura che diventeranno fiocchi sono impaccate all’interno della nuvola. Keplero esamina allora gli impaccamenti di sfere nello spazio. Ne riconosce due (a sinistra nella figura) e focalizza l’attenzione sulla distribuzione B, in cui ogni sfera ne tocca altre dodici; parla di questa configurazione come della più densa possibile. Questa affermazione, che il Nostro butta lì così, verrà chiamata congettura di Keplero.

La densità dell’impaccamento B è π/(3√2) ≈ 0,74. Mentre è chiaro che il reticolo esagonale nel piano, che possiamo riprodurre con un po’ di monete, sia il più denso possibile, nello spazio resta il dubbio: sarà proprio vero che la configurazione B sia la più densa realizzabile? Il problema della forma dei fiocchi di neve passa in secondo piano; quale sia l’impaccamento di sfere più denso, invece, è un quesito che appassionerà matematici di tutte le epoche successive. Ci vuole il grande Karl Friedrich Gauss per dimostrare, nel 1831, che effettivamente Keplero ha ragione, ma limitatamente a impaccamenti regolari, che si ripetono nello spazio come carta da parati nel piano. La dimostrazione definitiva per impaccamenti anche irregolari arriva solo nel 2014, ad opera di Thomas C. Hales.

Ma intanto la fantasia dei matematici si è scatenata. Si studiano varianti della congettura in geometrie non euclidee e nelle dimensioni superiori. Nel 1958 Carl A. Rogers presenta una formula che fornisce, per ogni dimensione, un limite superiore (“confine di Rogers”) alla densità di un impaccamento di sfere. Si inventano impaccamenti che generalizzano la configurazione B a tutte le dimensioni. Di particolare interesse è il reticolo ideato da John Leech nel 1967.

Comprensibilmente il lettore si chiederà: ma che senso ha occuparsi di sfere (più correttamente: ipersfere) in dimensioni superiori alle nostre tre? La risposta arriva, quando la teoria è già sviluppata, da un problema informatico molto importante. Ogni segnale, quando viene trasmesso attraverso Internet, ma anche da calcolatore a stampante e perfino all’interno del computer, subisce corruzioni: inevitabilmente c’è qualche bit 0 che diventa 1 o viceversa. Si sono allora studiate tecniche di correzione automatica degli errori più probabili. Una di queste tecniche consiste nel piazzare le “parole”, ammesse come valide, all’interno di spazi astratti di dimensione elevata. Se la parola viene alterata nella trasmissione, viene trasformata (con alta probabilità) in una parola non valida presente nello stesso spazio, ma vicina alla parola originaria. Il trucco consiste allora nel trasformare a posteriori la parola corrotta nella parola valida più vicina. Cioè: si costruisce una ipersfera centrata su ogni parola valida; la parola corrotta finisce in una di queste ipersfere e il sistema la sostituisce col suo centro.

Tutte le dimensioni sono ugualmente buone per realizzare questo metodo? No! Quanto più denso è un impaccamento di ipersfere, tanto più efficiente è il sistema di correzione di errori. Bene, nel 2004 si è scoperto che il reticolo di Leech ha un andamento della densità in funzione della dimensione molto particolare (a destra nella figura) e che nella dimensione 24 è decisamente il più conveniente. Una volta di più la curiosità e la fantasia dei matematici sono state ricompensate, anche se nate da uno scherzoso omaggio ispirato da un fiocco di neve.