Fibonacci day, la storia di una successione che ebbe fortuna secoli dopo

Dal 23 al 26 novembre Pisa celebra Leonardo Pisano, detto Fibonacci (cioè figlio di Bonaccio). La data si riferisce a quella, solo convenzionale, della sua nascita e viene dall’uso americano di indicare prima il mese poi il giorno: 11/23 – data scelta perché 1, 1, 2, 3 sono i primi numeri della famosa successione, di cui parlo più avanti. Un’americanata pazzesca come il giorno di pi greco, ma pazienza: ben venga ogni iniziativa che fa parlare della matematica e, in questo caso, di un importante matematico italiano.

Leonardo nacque e morì a Pisa (circa 1170 – circa 1242) e in mezzo viaggiò molto, soprattutto nell’evoluto dominio musulmano, dall’Algeria alla Siria. Non si sa se l’altro suo soprannome, “Bigollo”, volesse dire “trottola” per questo suo viaggiare, o “bighellone” per il fatto che perdeva tempo con la matematica invece di fare quattrini. Il suo contributo più importante è senz’altro il Liber abaci, in cui promuove per primo la diffusione del metodo posizionale, appreso proprio in Algeria; un metodo che ha semplicemente rivoluzionato tutta la matematica e la scienza europee.

Mi spiego: si trattava di passare dalla numerazione romana a quella che usiamo tuttora, con l’ultima cifra per le unità, la penultima per le decine eccetera, con la sconvolgente novità della cifra zero. Questo ci consente algoritmi (tranquilli: vuol dire “procedimenti di calcolo”) molto più snelli: provate a fare addizioni e moltiplicazioni con i numeri romani! Il primo impatto fu sulla ragioneria, e non è poco, ma poi tutta la scienza ne trasse un vantaggio enorme.

Leonardo Pisano si occupò anche di geometria, sulla scia della tradizione greca, ma le sue opere più feconde sono quelle su problemi algebrici, in cui risulta precursore della fenomenale fioritura rinascimentale, che pose quelle che oggi si chiamano Toscana, Emilia-Romagna, Veneto e Lombardia al centro del mondo matematico e scientifico.

La “tenzone di Palermo”, vinta da lui, ci dà una misura della differenza culturale fra il suo secolo e il nostro. È vero che allora la stragrande maggioranza della popolazione era analfabeta; in questo, il nostro tempo è incredibilmente migliore (e vorrei che lo fosse ancora di più). Allora, però, alla corte palermitana di Federico II c’era spazio per una tenzone relativa a una particolare equazione di terzo grado, che Fibonacci risolse con un’ottima approssimazione. Immaginate una qualsiasi “corte” moderna in cui nasca un interesse del genere?

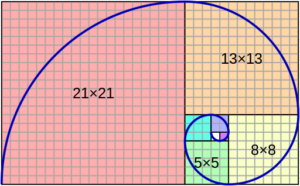Ma veniamo alla celebre successione. È data dai numeri F(n), dove F(1)=F(2)=1 e, per ogni n>2, F(n)=F(n-1)+F(n-2). Ecco i suoi primi elementi: 1, 1, 2, 3, 5, 8, 13, 21 eccetera. Nasce da un problema enunciato e risolto nel Liber abaci. Assumendo 1) di avere, al mese numero uno, una coppia di conigli maschio e femmina neonati; 2) che ogni coniglio neonato diventi fertile dopo un mese esatto, 3) che ogni mese da ogni coppia fertile nasca una coppia maschio-femmina, 4) che per un bel po’ non muoia nessuno, si chiede: al mese numero n, quante coppie di conigli ci sono? Facciamo le prove (anzi: ragioniamo) e vedremo che la risposta è proprio F(n) definito sopra.

A parte la novità di un procedimento ricorsivo, che investe tanta parte della matematica e dell’informatica, la cosa sensazionale è la varietà di situazioni in cui si trovano numeri della successione. Contate le spirali destrorse e sinistrorse di fiorellini in un girasole: sono due numeri consecutivi F(n) e F(n+1). Idem per le spirali di scaglie in una pigna o di infiorescenze nel broccolo romano o in un cactus. I numeri di petali di molti fiori sono numeri della successione. Le applicazioni recenti all’informatica e all’economia hanno dell’incredibile.

Però la vera porta dalla successione di Fibonacci al mondo viene da un’osservazione che Johannes Kepler fece quattro secoli dopo. Facciamo il rapporto fra due elementi consecutivi della successione: 1/1, 2/1, 3/2, 5/3, 8/5 eccetera; Kepler capì e dimostrò che la frazione F(n+1)/F(n), al crescere di n, approssima sempre meglio un numero celebre fin dall’antichità, la “sezione aurea” phi, che è davvero ubiquitaria nell’arte, nella natura, nelle applicazioni. Fa parte della magia della matematica il fatto che i suoi fili si riallaccino a distanza di secoli, che un’idea nata per gioco o per curiosità trovi applicazioni in un mondo totalmente diverso da quello in cui è sorta. Leonardo Pisano Bigollo Fibonacci è senz’altro un degno personaggio di questo affascinante romanzo di avventura.